Stack Data Structure (Introduction and Program)
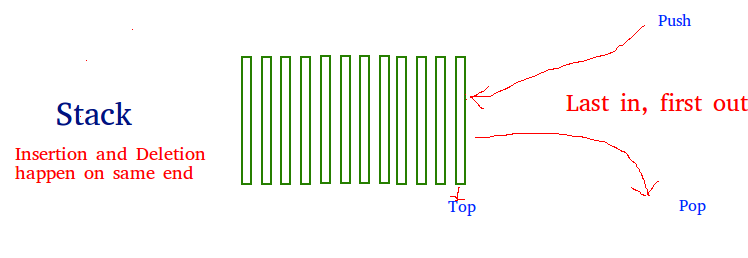
Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
Mainly the following three basic operations are performed in the stack:
- Push: Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
- Pop: Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
- Peek or Top: Returns top element of stack.
- isEmpty: Returns true if stack is empty, else false.
How to understand a stack practically?
There are many real-life examples of a stack. Consider the simple example of plates stacked over one another in a canteen. The plate which is at the top is the first one to be removed, i.e. the plate which has been placed at the bottommost position remains in the stack for the longest period of time. So, it can be simply seen to follow LIFO/FILO order.
Time Complexities of operations on stack:
push(), pop(), isEmpty() and peek() all take O(1) time. We do not run any loop in any of these operations.
Applications of stack:
- Balancing of symbols
- Infix to Postfix /Prefix conversion
- Redo-undo features at many places like editors, photoshop.
- Forward and backward feature in web browsers
- Used in many algorithms like Tower of Hanoi, tree traversals, stock span problem, histogram problem.
- Other applications can be Backtracking, Knight tour problem, rat in a maze, N queen problem and sudoku solver
- In Graph Algorithms like Topological Sorting and Strongly Connected Components
Implementation:
There are two ways to implement a stack:
- Using array
- Using linked list
Pros: Easy to implement. Memory is saved as pointers are not involved.
Cons: It is not dynamic. It doesn’t grow and shrink depending on needs at runtime.
Output :
10 pushed into stack 20 pushed into stack 30 pushed into stack 30 popped from stack
10 pushed to stack 20 pushed to stack 30 pushed to stack 30 popped from stack Top element is 20
Pros: The linked list implementation of stack can grow and shrink according to the needs at runtime.
Cons: Requires extra memory due to involvement of pointers.
Stack | Set 2 (Infix to Postfix)
Prerequisite – Stack | Set 1 (Introduction)
Infix expression:The expression of the form a op b. When an operator is in-between every pair of operands.
Postfix expression:The expression of the form a b op. When an operator is followed for every pair of operands.
Why postfix representation of the expression?
The compiler scans the expression either from left to right or from right to left.
Consider the below expression: a op1 b op2 c op3 d
If op1 = +, op2 = *, op3 = +
The compiler first scans the expression to evaluate the expression b * c, then again scan the expression to add a to it. The result is then added to d after another scan.
The repeated scanning makes it very in-efficient. It is better to convert the expression to postfix(or prefix) form before evaluation.
The corresponding expression in postfix form is: abc*+d+. The postfix expressions can be evaluated easily using a stack. We will cover postfix expression evaluation in a separate post.
Algorithm
1. Scan the infix expression from left to right.
2. If the scanned character is an operand, output it.
3. Else,
…..3.1 If the precedence of the scanned operator is greater than the precedence of the operator in the stack(or the stack is empty or the stack contains a ‘(‘ ), push it.
…..3.2 Else, Pop all the operators from the stack which are greater than or equal to in precedence than that of the scanned operator. After doing that Push the scanned operator to the stack. (If you encounter parenthesis while popping then stop there and push the scanned operator in the stack.)
4. If the scanned character is an ‘(‘, push it to the stack.
5. If the scanned character is an ‘)’, pop the stack and and output it until a ‘(‘ is encountered, and discard both the parenthesis.
6. Repeat steps 2-6 until infix expression is scanned.
7. Print the output
8. Pop and output from the stack until it is not empty.
// C program to convert infix expression to postfix
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
// Stack type
struct Stack
{
int top;
unsigned capacity;
int* array;
};
// Stack Operations
struct Stack* createStack( unsigned capacity )
{
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
if (!stack)
return NULL;
stack->top = -1;
stack->capacity = capacity;
stack->array = (int*) malloc(stack->capacity * sizeof(int));
return stack;
}
int isEmpty(struct Stack* stack)
{
return stack->top == -1 ;
}
char peek(struct Stack* stack)
{
return stack->array[stack->top];
}
char pop(struct Stack* stack)
{
if (!isEmpty(stack))
return stack->array[stack->top--] ;
return '$';
}
void push(struct Stack* stack, char op)
{
stack->array[++stack->top] = op;
}
// A utility function to check if the given character is operand
int isOperand(char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}
// A utility function to return precedence of a given operator
// Higher returned value means higher precedence
int Prec(char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
return 3;
}
return -1;
}
// The main function that converts given infix expression
// to postfix expression.
int infixToPostfix(char* exp)
{
int i, k;
// Create a stack of capacity equal to expression size
struct Stack* stack = createStack(strlen(exp));
if(!stack) // See if stack was created successfully
return -1 ;
for (i = 0, k = -1; exp[i]; ++i)
{
// If the scanned character is an operand, add it to output.
if (isOperand(exp[i]))
exp[++k] = exp[i];
// If the scanned character is an ‘(‘, push it to the stack.
else if (exp[i] == '(')
push(stack, exp[i]);
// If the scanned character is an ‘)’, pop and output from the stack
// until an ‘(‘ is encountered.
else if (exp[i] == ')')
{
while (!isEmpty(stack) && peek(stack) != '(')
exp[++k] = pop(stack);
if (!isEmpty(stack) && peek(stack) != '(')
return -1; // invalid expression
else
pop(stack);
}
else // an operator is encountered
{
while (!isEmpty(stack) && Prec(exp[i]) <= Prec(peek(stack)))
exp[++k] = pop(stack);
push(stack, exp[i]);
}
}
// pop all the operators from the stack
while (!isEmpty(stack))
exp[++k] = pop(stack );
exp[++k] = '\0';
printf( "%s", exp );
}
// Driver program to test above functions
int main()
{
char exp[] = "a+b*(c^d-e)^(f+g*h)-i";
infixToPostfix(exp);
return 0;
}
Output:
abcd^e-fgh*+^*+i-
Stack | Set 3 (Reverse a string using stack)
Given a string, reverse it using stack. For example “GeeksQuiz” should be converted to “ziuQskeeG”.
Following is simple algorithm to reverse a string using stack.
1) Create an empty stack. 2) One by one push all characters of string to stack. 3) One by one pop all characters from stack and put them back to string.
Reversed string is ziuQskeeG
Time Complexity: O(n) where n is number of characters in stack.
Auxiliary Space: O(n) for stack.
A string can also be reversed without using any auxiliary space. Following C, Java, C# and Python programs to implement reverse without using stack.
// C program to reverse a string without using stack
#include <stdio.h>
#include <string.h>
// A utility function to swap two characters
void swap(char *a, char *b)
{
char temp = *a;
*a = *b;
*b = temp;
}
// A stack based function to reverse a string
void reverse(char str[])
{
// get size of string
int n = strlen(str), i;
for (i = 0; i < n/2; i++)
swap(&str[i], &str[n-i-1]);
}
// Driver program to test above functions
int main()
{
char str[] = "abc";
reverse(str);
printf("Reversed string is %s", str);
return 0;
}
Output:
Reversed string is cba
Stack | Set 4 (Evaluation of Postfix Expression)
The Postfix notation is used to represent algebraic expressions. The expressions written in postfix form are evaluated faster compared to infix notation as parenthesis are not required in postfix. We have discussed infix to postfix conversion. In this post, evaluation of postfix expressions is discussed.
Following is algorithm for evaluation postfix expressions.
1) Create a stack to store operands (or values).
2) Scan the given expression and do following for every scanned element.
…..a) If the element is a number, push it into the stack
…..b) If the element is a operator, pop operands for the operator from stack. Evaluate the operator and push the result back to the stack
3) When the expression is ended, the number in the stack is the final answer.
Example:
Let the given expression be “2 3 1 * + 9 -“. We scan all elements one by one.
1) Scan ‘2’, it’s a number, so push it to stack. Stack contains ‘2’
2) Scan ‘3’, again a number, push it to stack, stack now contains ‘2 3’ (from bottom to top)
3) Scan ‘1’, again a number, push it to stack, stack now contains ‘2 3 1’
4) Scan ‘*’, it’s an operator, pop two operands from stack, apply the * operator on operands, we get 3*1 which results in 3. We push the result ‘3’ to stack. Stack now becomes ‘2 3’.
5) Scan ‘+’, it’s an operator, pop two operands from stack, apply the + operator on operands, we get 3 + 2 which results in 5. We push the result ‘5’ to stack. Stack now becomes ‘5’.
6) Scan ‘9’, it’s a number, we push it to the stack. Stack now becomes ‘5 9’.
7) Scan ‘-‘, it’s an operator, pop two operands from stack, apply the – operator on operands, we get 5 – 9 which results in -4. We push the result ‘-4’ to stack. Stack now becomes ‘-4’.
8) There are no more elements to scan, we return the top element from stack (which is the only element left in stack).
// C program to evaluate value of a postfix expression
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
// Stack type
struct Stack
{
int top;
unsigned capacity;
int* array;
};
// Stack Operations
struct Stack* createStack( unsigned capacity )
{
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
if (!stack) return NULL;
stack->top = -1;
stack->capacity = capacity;
stack->array = (int*) malloc(stack->capacity * sizeof(int));
if (!stack->array) return NULL;
return stack;
}
int isEmpty(struct Stack* stack)
{
return stack->top == -1 ;
}
char peek(struct Stack* stack)
{
return stack->array[stack->top];
}
char pop(struct Stack* stack)
{
if (!isEmpty(stack))
return stack->array[stack->top--] ;
return '$';
}
void push(struct Stack* stack, char op)
{
stack->array[++stack->top] = op;
}
// The main function that returns value of a given postfix expression
int evaluatePostfix(char* exp)
{
// Create a stack of capacity equal to expression size
struct Stack* stack = createStack(strlen(exp));
int i;
// See if stack was created successfully
if (!stack) return -1;
// Scan all characters one by one
for (i = 0; exp[i]; ++i)
{
// If the scanned character is an operand (number here),
// push it to the stack.
if (isdigit(exp[i]))
push(stack, exp[i] - '0');
// If the scanned character is an operator, pop two
// elements from stack apply the operator
else
{
int val1 = pop(stack);
int val2 = pop(stack);
switch (exp[i])
{
case '+': push(stack, val2 + val1); break;
case '-': push(stack, val2 - val1); break;
case '*': push(stack, val2 * val1); break;
case '/': push(stack, val2/val1); break;
}
}
}
return pop(stack);
}
// Driver program to test above functions
int main()
{
char exp[] = "231*+9-";
printf ("postfix evaluation: %d", evaluatePostfix(exp));
return 0;
}
postfix evaluation: -4
Time complexity of evaluation algorithm is O(n) where n is number of characters in input expression.
There are following limitations of above implementation.
1) It supports only 4 binary operators ‘+’, ‘*’, ‘-‘ and ‘/’. It can be extended for more operators by adding more switch cases.
2) The allowed operands are only single digit operands. The program can be extended for multiple digits by adding a separator like space between all elements (operators and operands) of given expression.
Below given is the extended program which allows operands having multiple digits.
// C program to evaluate value of a postfix
// expression having multiple digit operands
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
// Stack type
struct Stack
{
int top;
unsigned capacity;
int* array;
};
// Stack Operations
struct Stack* createStack( unsigned capacity )
{
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
if (!stack) return NULL;
stack->top = -1;
stack->capacity = capacity;
stack->array = (int*) malloc(stack->capacity * sizeof(int));
if (!stack->array) return NULL;
return stack;
}
int isEmpty(struct Stack* stack)
{
return stack->top == -1 ;
}
int peek(struct Stack* stack)
{
return stack->array[stack->top];
}
int pop(struct Stack* stack)
{
if (!isEmpty(stack))
return stack->array[stack->top--] ;
return '$';
}
void push(struct Stack* stack,int op)
{
stack->array[++stack->top] = op;
}
// The main function that returns value
// of a given postfix expression
int evaluatePostfix(char* exp)
{
// Create a stack of capacity equal to expression size
struct Stack* stack = createStack(strlen(exp));
int i;
// See if stack was created successfully
if (!stack) return -1;
// Scan all characters one by one
for (i = 0; exp[i]; ++i)
{
//if the character is blank space then continue
if(exp[i]==' ')continue;
// If the scanned character is an
// operand (number here),extract the full number
// Push it to the stack.
else if (isdigit(exp[i]))
{
int num=0;
//extract full number
while(isdigit(exp[i]))
{
num=num*10 + (int)(exp[i]-'0');
i++;
}
i--;
//push the element in the stack
push(stack,num);
}
// If the scanned character is an operator, pop two
// elements from stack apply the operator
else
{
int val1 = pop(stack);
int val2 = pop(stack);
switch (exp[i])
{
case '+': push(stack, val2 + val1); break;
case '-': push(stack, val2 - val1); break;
case '*': push(stack, val2 * val1); break;
case '/': push(stack, val2/val1); break;
}
}
}
return pop(stack);
}
// Driver program to test above functions
int main()
{
char exp[] = "100 200 + 2 / 5 * 7 +";
printf ("%d", evaluatePostfix(exp));
return 0;
}
Output :
757
thnks sir
ReplyDelete